LearnR Tutorial

Linear Regression

Simple Linear Regression

One of the most frequent used techniques in statistics is linear regression. Linear regression or ordinary least squares (OLS) investigates the relationship between one or more variables (independent variables) and a variable of interest (dependent variable).

Here, we use the pokemon dataset to explore the relationship between pokemons’ weight and strength of attack. First, we would like to visualise how our pokemons are distributed along these two dimensions. We use ggplot() to create a scatterplot:

  ggplot(data=pokemon, aes(height_m, weight_kg))+
  geom_point(alpha=.5, color='black')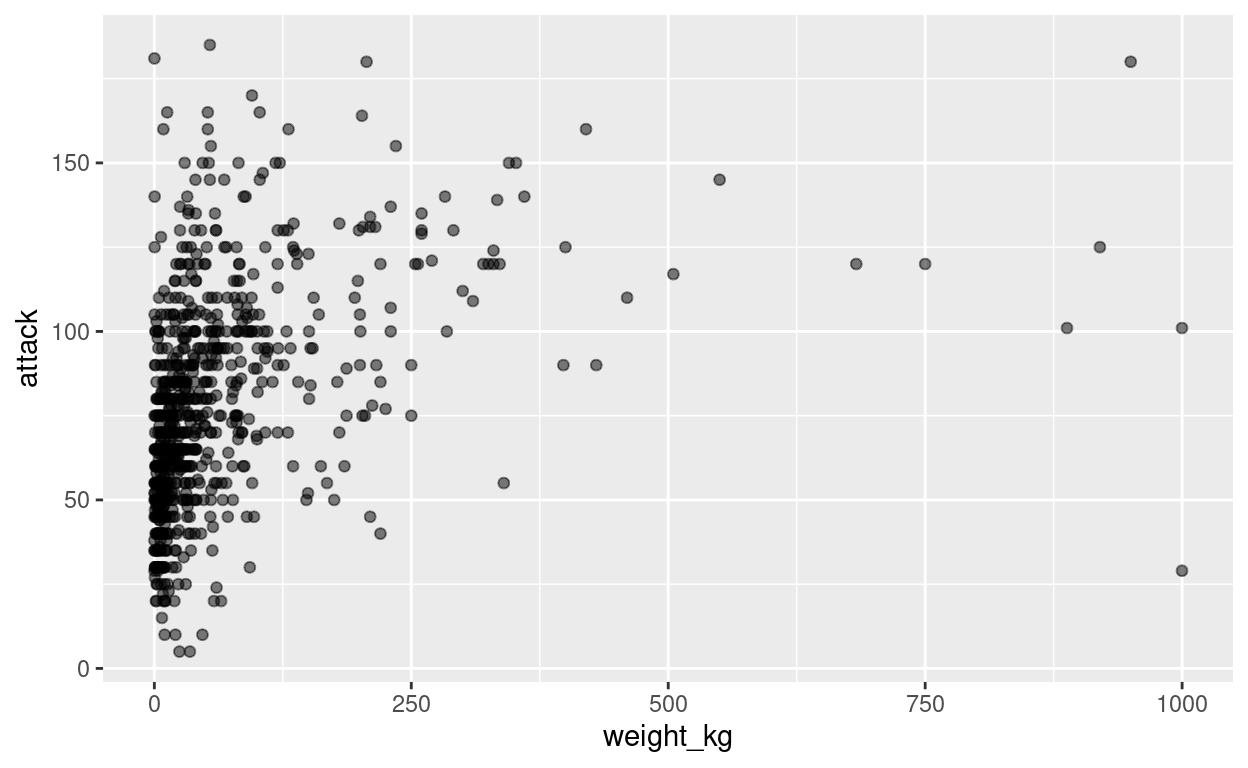

The formula for this linear regression is: \[y = \beta_0 + \beta_1x\] where \(y\) is the dependent variable (attack), \(x\) the independent variable (weight_kg), \(\beta_0\) the intercept and \(\beta_1\) the slope of the line.

In R we can fit a linear model to the data with the function lm(). The dependent and independent variable(s) are separated by a tilde ~, and the name of the dataset as an argument.

Try to write code for a linear regression with weight predicting strength of attack of a pokemon

lm(attack ~ weight_kg, pokemon)

The intercept refers to the expected value of \(y\) when \(x=0\) whereas the coefficient \(\beta_1\) is the slope of the regression line. The slope describes the mean change in \(y\) for each 1-unit increase in \(x\). Please note that the intercept or base rate depends on the coding of the independent variable (i.e, dummy, deviaton coding)

We can add a regression line to our scatterplot with geom_smooth(), since we have already specified the variables of interest in ggplot, we just need to specify linear model as the method used here, written as method='lm'.

Complete the code to add the regression line to the plot (you might want to use another color for the line)

ggplot(pokemon, aes(weight_kg, attack)) +
  geom_point(alpha=.5, color='black') +
  geom_smooth()

ggplot(pokemon, aes(weight_kg, attack)) +
  geom_point(alpha=.5, color='black') +
  geom_smooth(method = 'lm', color='blue')

Confidence interval

Note that this command also added a 95% confidence interval to the regresson line by default. The ‘shadow’ around the line reflects the uncertainty in our estimate of intercept and slope.

Multiple Linear Regression

If we want to study the combined effect of two or more independent variables, we can run a regression with multiple predictors.

In our pokemon dataset, we might want to see whether there is an effect of pokemons’ height on attack, as well. In the notation of lme4 package, we add predictors to a linear model with the “+” operator.

Complete the code by adding the independent variable height (height_m) to the model

lm(attack ~ weight_kg, pokemon)

lm(attack ~ weight_kg + height_m, pokemon)

If we have more than one predictor variable, it is no longer straightforward to visualise a regression (for that you may use partial regressions). But we still have the coefficients to help us: In this example we can see that if both height and weight are zero the expected attack strength of a pokemon is around 64, then, for each additional kg of weight there is an expected increase in attack strength of about 0.06 points, whereas for each meter in height an expected increase of about 9.0 points.

Quiz

Some questions to verify that you understand the use of linear regression.

Quiz

Anscombe Quartet

Linear Digressions

The following four datasets were developed by Anscombe (1973). They illustrate the importance of graphical representations to understand relationships between variables.

Choose a Dataset

Dataset

Raw data, and statistics

The differences between the four data sets in terms of mean, variance, and correlation are very small.

Anscome Quartet

Plotting the data sets reveals the differences between the linear fits. Explore the data by clicking on individual data points to exclude them from the regression. A second click or clicking the reset button at the bottom restores the values.

Quiz

Some questions to verify that you understand the differences between the data sets:

Quiz

Logistic Regression

Why Logistic Regression?

Logistic regression is used to predict binary events with only two mutually exclusive outcomes. This is the same as a classification into two categories.
Here are a few examples of binary events, such as tossing a coin, test for diabetes, and fatality of a stroke:

Continuous variables, such as 'time' or 'height' as well as categorical variables, such as 'school' or 'gender' can be used as predictors for these outcomes.

Type

Choose one

Probability p to odds

Probability p to log_odds

Why transform to log odds?

When the probability p approaches 1, the odds p/(1-p) increase exponentially towards infinity (red circle). In order to use linear regression for prediction a non-linear, more 'well-behaved' transformation is preferred. The logistic function transforms probabilities from the range of 0 and 1.

Quiz

Some questions to verify that you understand the purpose and use of logistic regression.

Quiz

Examples

Here we provide two example data sets. The first one looks at prevalence of diabetes among Pima Indians using different risk factors as predictors of diabetes. The other data set describes passengers of the Titanic on its final voyage and looks at factors that might have affected their survival. On the y-axis '1' means diabetes or survival, '0' means no diabetes or no survival. The histogramms at the top or bottom represent the number of cases for each level of the factor that fall into the binary category. So the top counts indians with diabetes or titanic survivors, while the bottom counts indians without diabetes or titanic casualties. If you want a more detailed representation for continous variables you can choose 'points' in the visualisation box.

Choose a dataset

Dataset

Choose a predictor

X Variable

Choose a visualization

Visualization

Histogram

Points

Data Visualisation

Quiz

Some questions to see what you have learned from the Titanic data set.

Quiz

Here we work with the dataset data_tit for survival of the sinking of the titanic. The predictor Sex is dummy-coded with 0=female and 1=male. The crosstable function xtabs(~Survived + Sex, data_tit) provides the observed frequencies. From the table compute the odds and probabilities of survival for female and male passengers and the log odds for female to male passengers.

xtabs(~Survived + Sex, data_tit)
odds_fm = 232/81
odds_m = 107/468
prob_fm = 223/(81+232)
prob_m = 107/(468+107)
odds_fm = odds_fm/odds_m
log(odds_fm)

Similar to a linear regression lm() we can fit a general linear model to the data with the function glm(). As before the binary dependent and independent variable(s) are separated by a tilde ~ followed by the name of the dataset data_tit as the first argument. In addition, we transform the probabilities of survival into log odds using the argument family="binomial".

Try to write code for a logistic regression with Sex predicting the log odds of Survived

glm1 = glm(Survived ~ Sex, data_tit, family="binomial")
summary(glm1)

If you call summary() of your model you get the coeficients. How to interpret the results? This depends on the coding of your independent variables.

Quiz

Some questions to see if you understand the output of the logistic regression.

Quiz

Add TicketPrice as another predictor to the model. Do the coefficients change?

Try to write code for a logistic regression with Sex and TicketPrice predicting the log odds of Survived

glm2 = glm(Survived ~ Sex + TicketPrice, data_tit, binomial(link = "logit") )
summary(glm2)

Compare the coefficiens with the observed numbers. Why have they changed?

Quiz

Some questions to see if you understand the output of the logistic regression.

Quiz

Mixed-effect Linear Regression

When do we use mixed-effect linear regression?

When our observations come from different groups or units, e.g. from subjects and items. This is relevant because some subjects perform better than others, and some items are easier than others. In our analyses, we want to take into account so-called “random” effects so that we get better estimates of “fixed” effects.

Mixed-effect models distinguish between “random” and “fixed” factors and their effects: A factor is called random when its levels are drawn randomly from a population, e.g., subjects from a population. Levels of a fixed factor are assumed to remain the same from one experiment to another and typically reflect experimental manipulations.

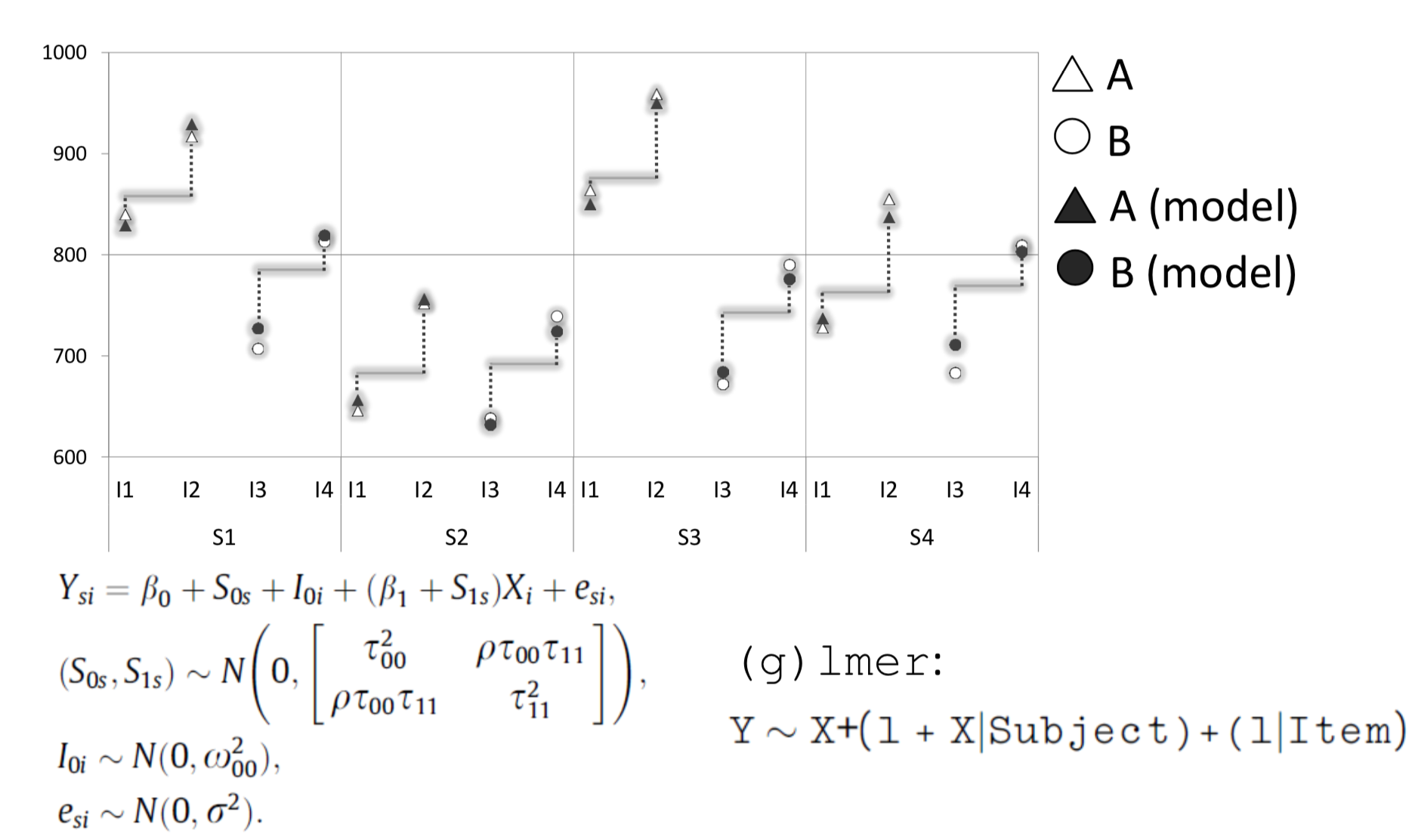
In the following example, borrowed from Barr et al. (2013), we look at a hypothetical experiment that examines the effect of “stimulus type” (A and B) on reaction times (RTs measured in ms). Our sample has only 4 subjects (S1 to S4) each of whom judged 4 items (I1 to I4). The resulting 16 data points are illustrated below.

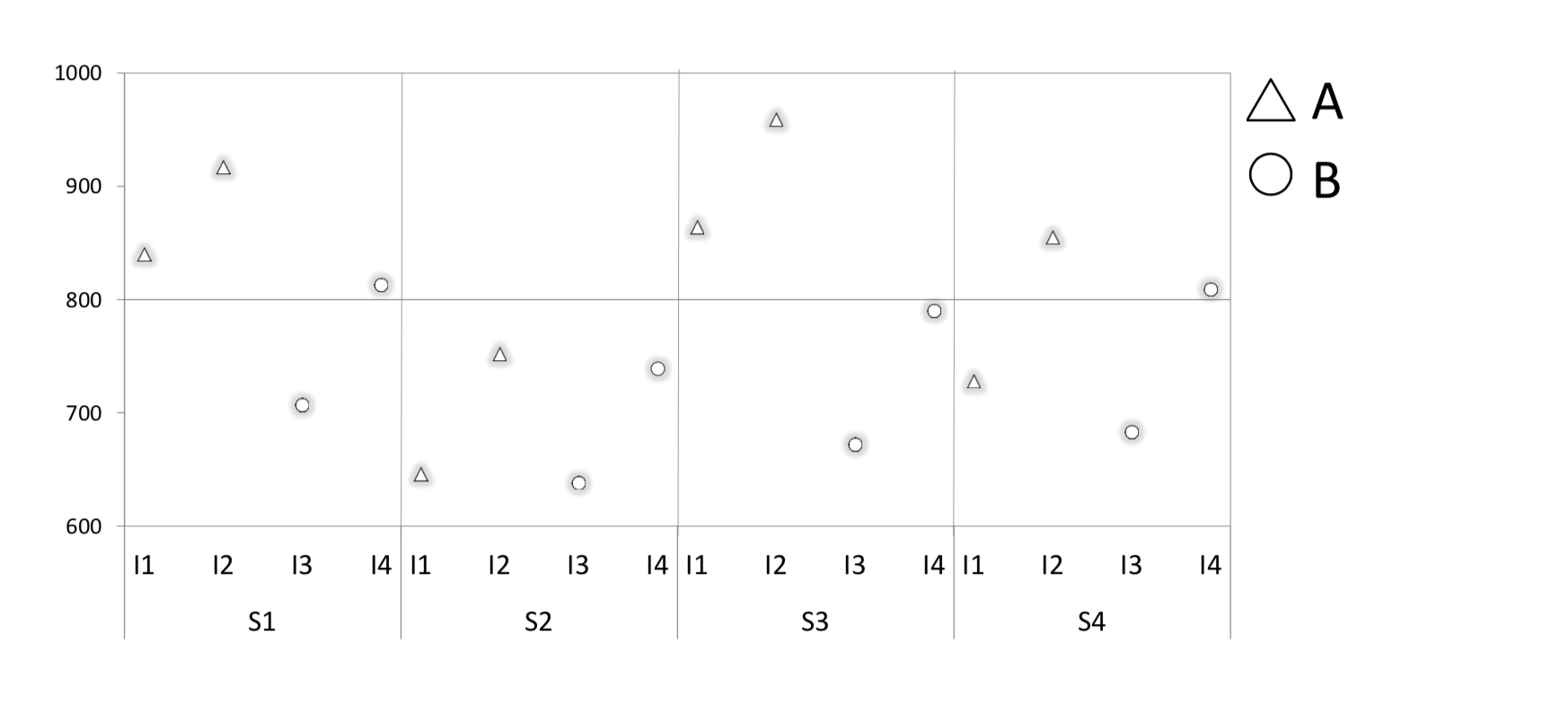
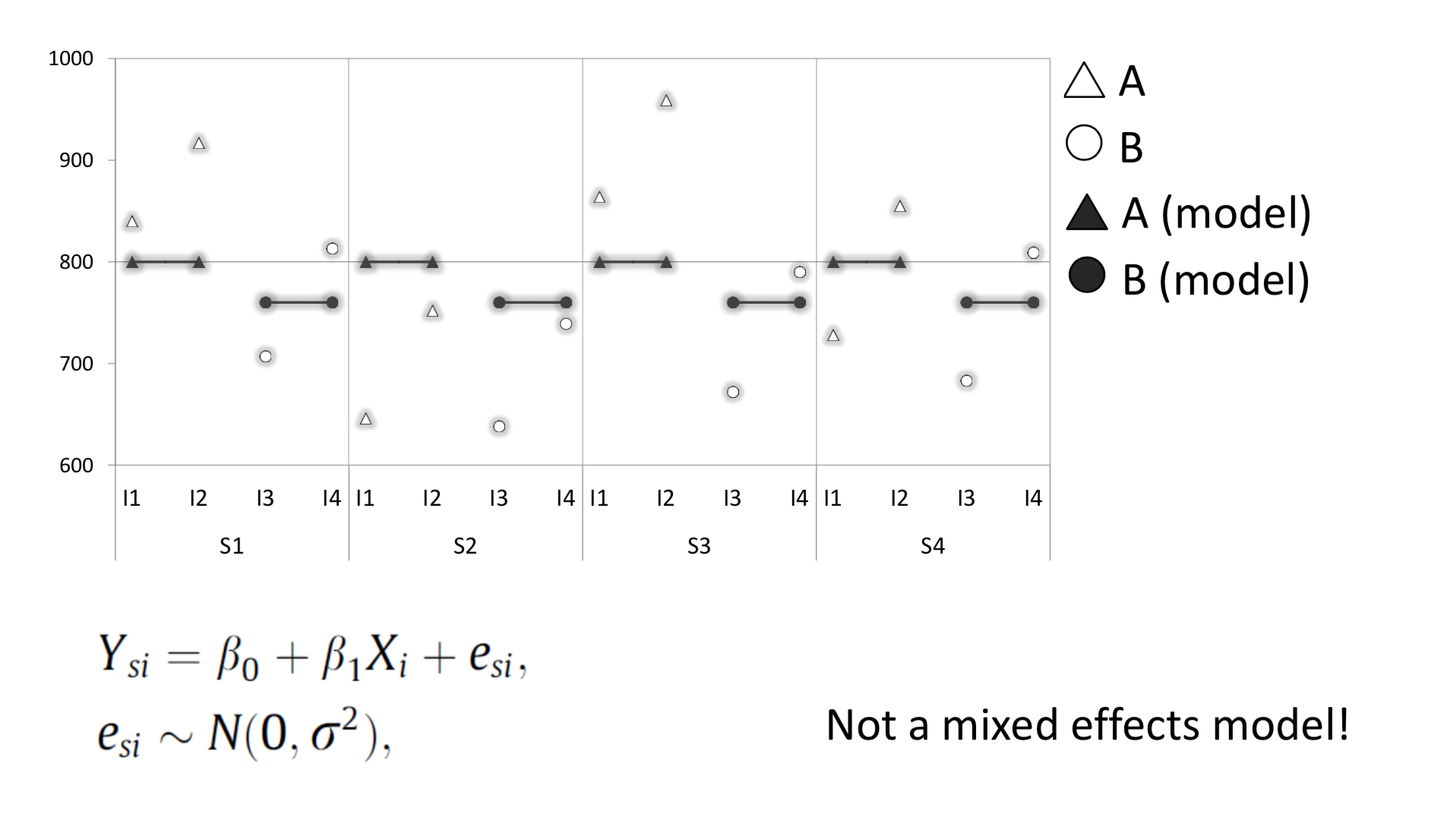
First, we conduct a simple linear regression that predicts the mean RT for each stimulus type independently of subjects and items.

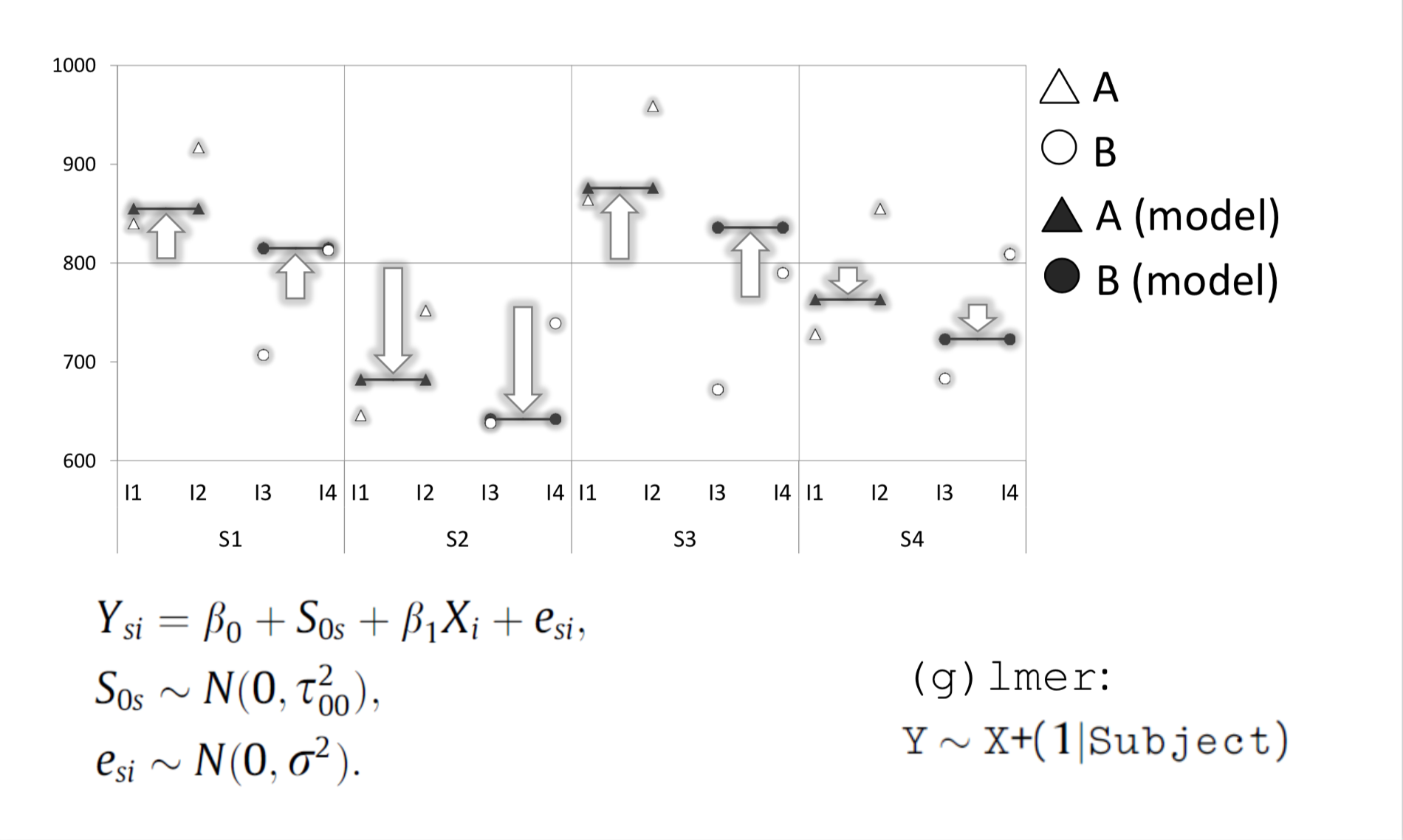
Next, we introduce a “random intercept” for each subject. Now we have a linear model with mixed-effects - where each subject has their own intercept.

By introducing by-subject “random slopes”, we can model the mean RT for each subject in each condition. The slope captures the change between condition A and B.

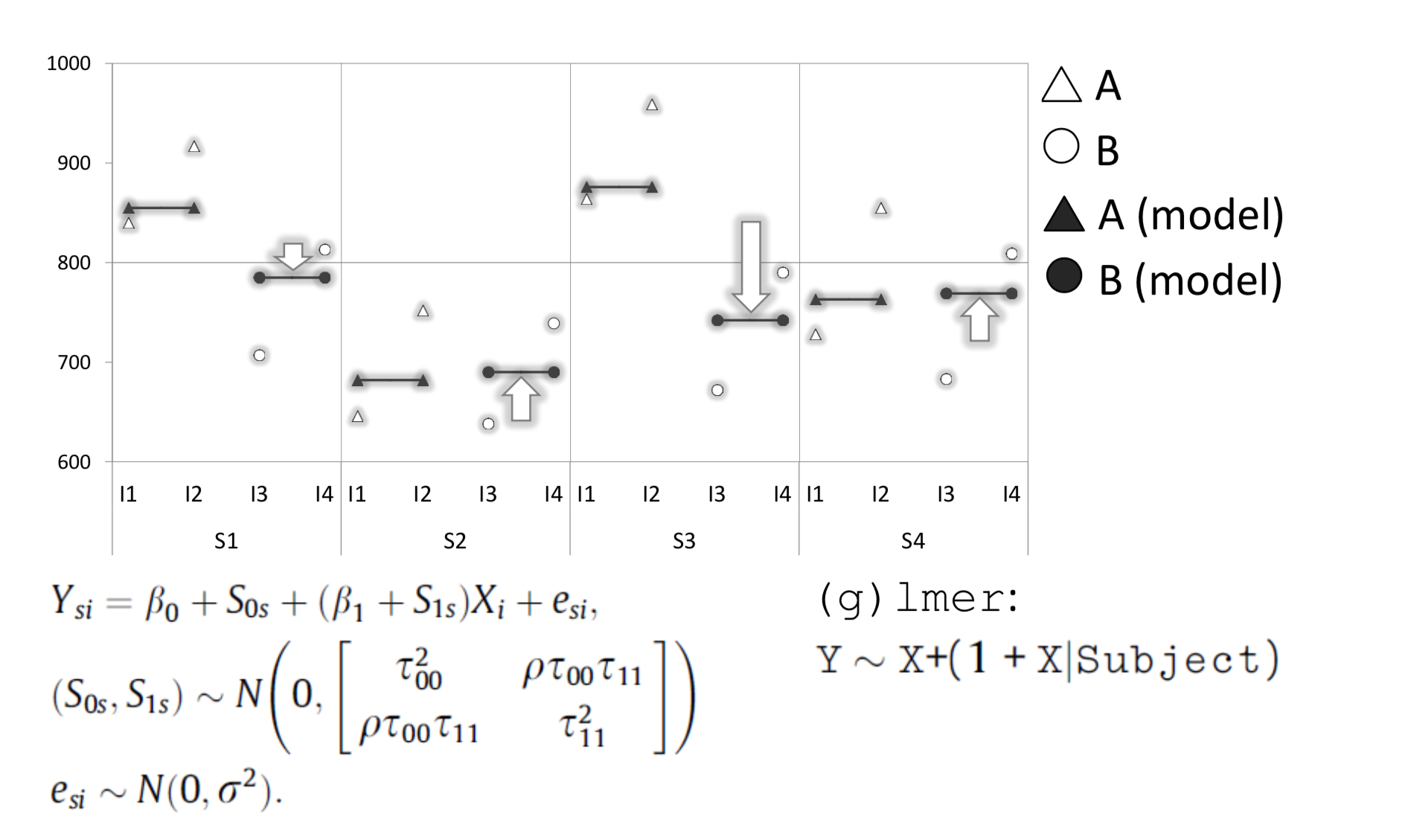
Finally, we introduce random intercepts for each item: This is the maximal model for the present experimental design. The model predictions correspond well with the original data points.

In the following interactive app you can create a new data set and see how different mixed-effects models fit the data.

Comparison of Linear Mixed Models based on likelihood ratio

Please specify the parameters of the dataset that you want to study. For example, if you set the fixed intercept to 8, this means that the grand mean of the dependent variable will be 8. Random effects are represented by their standard deviations. These values can only be positive. If you set the correlation between the random intercept and the random slope to zero, then they are independent. Once you generate the data you will see the first rows of the dataset. Then you can select a model from the list below and see how it fits your data. In order to compare two models select a second model from the list and the output will appear next to the previous.

How many subjects?

How many items?

Which fixed intercept do you want to use?

Which fixed slope do you want to use?

Which standard deviation do you want to use for the distribution of the random intercepts (subjects)?

Which standard deviation do you want to use for the distribution of the random slopes (subjects)?

Which correlation between intercept and slope do you want to use (subjects)?

Which standard deviation do you want to use for the distribution of the residual error?

Generated dataset

Likelihood Ratio Test and Model Comparison Deviance

Is the ChiSq-value significant (p-value)?

Quiz

Some questions to verify that you understand the purpose and use of linear mixed models:

Quiz