Combining Clustering and PCA

Now that you have learned the basics of clustering lets try a more complex example! When working with large data sets like the PISA data it is likely that you will want to cluster based on more than two variables. We could, therefore, cluster based on all the variables in the original countrySummary data we loaded in. However, this would be a very high-dimensional analysis since there are 26 variables in total. In instances where you are working with high-dimensional data it is possible to combine both PCA and Clustering.

PCA is first used to reduce the dimension of the data set, like you learned to do in the PCA section. Then instead of clustering based on the original variables you cluster based on the principle components. Using this method can lead to more stable clustering when you are working with a large data set like PISA. For more information see Husson, Josse & Pages, (2010)

In the first section you ran a PCA analysis on 7 teacher-related variables and determined that keeping the first 4 principle components was sufficient. In this section you will use your new clustering knowledge to run clustering analyses (k-means, hierarchical and DBSCAN) based on these 4 principle components. To do this we first need to extract the PCA data:

#extract pca data table 
teach_pca_dat <- as_tibble(teach_pca[["x"]]) %>% 
  #select relevent pcs
  select(PC1, PC2, PC3, PC4) %>%
  #add country information back in
  mutate(Country = teach_dat$Country)

K-means on PCA

Now that we have the country data as it relates to the principle components we can run our clustering analysis. The first analysis will be k-means. As there are more than 2 variables visualizing the data in a conventional 2-D scatter plot is not possible.

Using what you learned in the previous clustering sections use the fviz_nbclust() package to run the elbow and and then the average silhouette method to determine the optimal value of \(k\)

#Look back at the {r manual elbow method} code chunk if you need to refresh your knowledge 

## DATA ##
#make sure you are using the right data set i.e. teach_pca_dat
#Make sure that you are only using the bullying and discipline columns of the data set i.e.  [,1:4]

## FUNCTION ##
#Make sure you have the correct value analysis method i.e. kmeans
#Make sure you have the correct method arguments i.e. "wss" silhouette"
#Make sure you are running the the elbow method first then silhouette

## FUNCTION ##
#Make sure you have the correct value analysis method i.e. kmeans
#Make sure you have the correct method arguments i.e. "wss" silhouette"
#Make sure you are running the the elbow method first then silhouette

# WARNING: next hint shows full solution

fviz_nbclust(teach_pca_dat[,1:4], kmeans, method = "wss")
fviz_nbclust(teach_pca_dat[,1:4], kmeans, method = "silhouette")

Quiz

Now that you know the optimal \(k\) use the kmod() function to run a \(k\)-means analysis. Set the outlier parameter \(l\) to 5.

#Look back at the {r kmod} code chunk if you need to refresh your knowledge

## DATA ##
#make sure you are using the right dataset i.e. teach_pca_dat
#Make sure that you are only using the bullying and discipline columns of the data set i.e.  [,1:4]

## FUNCTION ##
#Make sure you have the correct value for k (opitmal k from previously) and l specified

# WARNING: next hint shows full solution

teach_kmod <- kmod(teach_pca_dat[,1:4], k=3, l=5)

We can also extract the countries that kmod treated as outliers:

#index country names of outliers from the l-index output
teach_pca_dat$Country[teach_kmod$L_index]

## [1] "Albania"            "Mexico"             "Brazil"            
## [4] "Morocco"            "Dominican Republic"

Interactive K-Means by Principle Components

It seems that the optimal parameters are k=3 for 4 components, however it is sometimes helpful to be able to visualise how these parameters interact with each other when making this decision. Here is an opportunity to play around with different values with and without outliers to see how this affects the clusters when plotted for PC1 and PC2.

Number of clusters:

Include outliers?

Number of Components:

Visualise Clusters on World Map

To better visualise what our clusters actually indicate, we can plot them on a map of the world. This will allow us to identify any trends that might be of interest, such as the grouping of countries that are geographically near each other or culturally similar. On the plot below you can see which countries have been grouped together. You can use the zoom and pan tools to see specific sections of the map in more detail:

Hierarchical Clustering on PCA

Now try and run hierarchical clustering on the PCA data. Use the hlcust function to run the the analysis with complete linkage. Assign your analysis to teach_hclust <-:

#Look back at the first line of code in the {r hclust complete} code chunk if you need to refresh your knowledge

## DATA ##
#Make sure you are using the right dataset i.e. teach_pca_dat
#Make sure that you are only using the bullying and discipline columns of the data set i.e.  [,1:4]
#Have you remember to compute the distance matrix of the data i.e. dist(teach_pca_dat[,1:4])
#Have you used the right linkage method i.e. method = "complete"
#Have you assigned the analysis correctly i.e. teach_hclust <-

## FUNCTION ##
#Have you remember to compute the distance matrix of the data i.e. dist(teach_pca_dat[,1:4])
#Have you used the right linkage method i.e. method = "complete"
#Have you assigned the analysis correctly i.e. teach_hclust <- 

# WARNING: next hint shows full solution

teach_hclust <- hclust(dist(teach_pca_dat[,1:4]), method="complete")

Now that you have ran the analysis we can visualise this on a dendrogram. You can see from the dendrogram that there seems to be 4 distint clusters:

teach_comp <- as.dendrogram(teach_hclust) %>%
  set("labels", teach_pca_dat$Country[teach_hclust$order])
plot(teach_comp, ylab = "Height", main = 'Complete Linkage')
rect.dendrogram(teach_comp, k = 4, border = 2:5)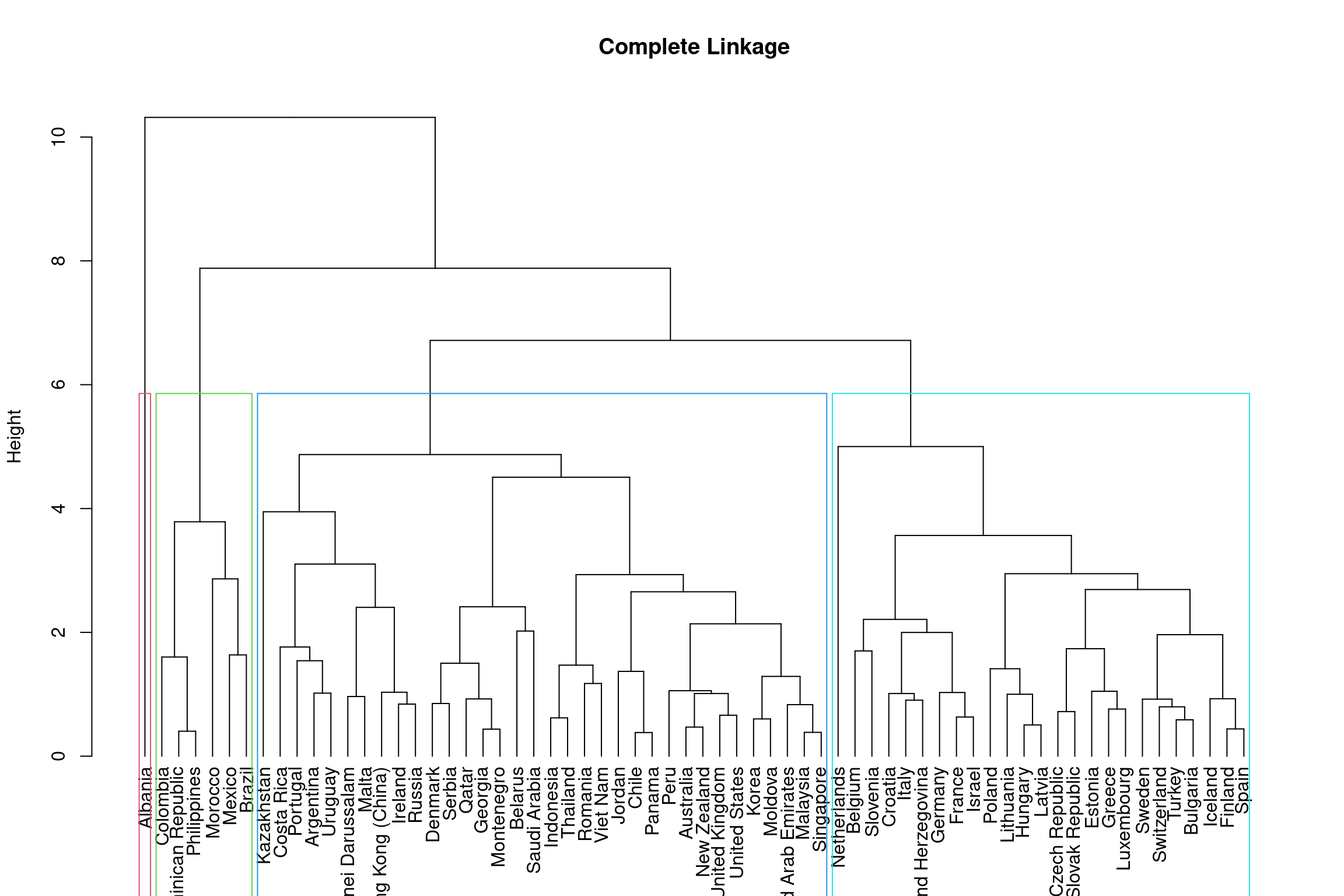

We can also plot these using the world map to compare the results with the k-means analysis:

You can see this method produces slightly different results to the k-means analysis and Albania is treated as it’s own cluster (zoom in on Europe).

DBSCAN on PCA

Finally lets run a DBSCAN analysis. You first need to determine \(\epsilon\). Use the kNNdistplot() function in the dbscan package. Set k to 3, h = 1 and lty = 2.

#Look back at the first line of code in the {r KNN elbow} code chunk if you need to refresh your knowledge

## DATA ##
#Make sure that you are calling the function properly i.e. dbscan::kNNdistplot()
#Make sure you are using the right dataset i.e. teach_pca_dat
#Make sure that you are only using the bullying and discipline columns of the data set i.e.  [,1:4]

## FUNCTION ##
#Make sure you have set k = 3
#To get the dashed line make sure you run abline(h = , lty = )

# WARNING: next hint shows full solution

dbscan::kNNdistplot(teach_pca_dat[,1:4], k = 3)
abline(h = 1.8, lty = 2)

Now that you have your plot change the value for h = and re-run in your code to move the dashed line around and find a logical value for \(\epsilon\). The elbow this time is not as definitive but this is where researcher decision making comes into play.

Quiz

Now that you have a value for \(\epsilon\) you can run the DSCAN analysis. Use the dbscan function in the fpc package to run the analysis and assign it to teach_db <-. Set MinPts to 3.

#Look back at the first line of code in the {r DBSCAN} code chunk if you need to refresh your knowledge

## DATA ##
#Make sure that you are calling the function properly i.e. fpc::dbscan()
#Make sure you are using the right dataset i.e. teach_pca_dat
#Make sure that you are only using the bullying and discipline columns of the data set i.e.  [,1:4]

#Make sure you have set eps = and MinPts to the correct values specified earlier i.e. eps = 1.8 and MinPts = 3

## FUNCTION ##
#Make sure you have set eps = and MinPts to the correct values specified earlier i.e. eps = 1.8 and MinPts = 3

# WARNING: next hint shows full solution

teach_db <- fpc::dbscan(teach_pca_dat[,1:4], eps = 1.8, MinPts = 3)

#runs density cluster analysis in background 
teach_db <- fpc::dbscan(teach_pca_dat[,1:4], eps = 1.8, MinPts = 3)

Once again this method has produced different country groupings than the k-means and hierarchical clustering methods. So how do you decide which solution to use? Unfortunately there is not a straight forwarded answer. We could compare the solutions using internal validity measures such as the Calinski-Harabasz index or silhouette values however the assumptions underlying these are more aligned with k-means and hierarchical clustering approaches. This means DBSCAN is likely to score lower than the other methods. There are other internal validation measures such as Density-Based Cluster Validation (DBCV) that align with DBSCAN, however k-means and hierarchical clustering are likely to score lower on these measures. For more information on why it is hard to fairly compare clustering approaches based on internal validation measures see Van Craenendonck & Blockeel (2015). Therefore, internal validation measures are best used for ensuring we set the right parameters. We could also use external validation such as cross validation, which will be covered in a later section.

In this instance it may be more intuitive to use the clustering solution that provides the most interpretable solution based on domain knowledge and research aim (i.e. what solution is the most interpretable and interesting given what we know about the culture and education systems of the countries included in our analysis).